Wireless

Binary Symmetric Channel

Jake

Apr 15, 2022 • 4 min read

The binary symmetric channel (BSC) is one of the simplest channel models to consider. It is usually the starting point when we begin to study information and coding theory. This model is really worth spending some time and effort to understand as it builds up the foundation for more complex channel models.

In this post, we want to go in-depth on the very basics of binary symmetric channels. We go through the essential properties of the binary symmetric channel. We will go through the following topics:

Go through the basic properties of the channel model.
Study how the channel model can be parametrized with just one parameter (transition/flip probability).
See how the transition probability affects the channel capacity.
Derive the commonly used capacity expression starting from the capacity definition vial the maximum mutual information.

The channel model

As the name says, a binary symmetric channel has two defining factors. First, it is binary, which means that it takes in only a binary alphabet. That is, we can only transmit binary symbols (0 or 1) through the channel. Similarly, the output messages are expected to be binary.

Second, the channel is symmetric. Regardless of the transmitted symbol, they both go through an identical transition process over the channel. This also means that, if we choose the input alphabets to be uniformly distributed also the output becomes uniformly distributed.

We can use an arbitrary distribution of the input symbols \(p_X(x)\) within the binary alphabet. However, from the capacity point of view, it is best to use uniform input distribution. We'll discuss more on this in the capacity deviation.

For each transmitted symbol, we have a transition probability \(p\), which determines the probability the transmitted symbol (bit) flips, which means that transmitted 0 is received as 1 or transmitted 1 is received as 0. This, of course, means that the probability of successful transmission is \(1 - p\). This also means that the transition process is parameterized by a single parameter \(p \in [0,1]\).

This model is also noiseless in the conventional sense as it does not contain a random additive noise process that corrupts the transmitted signal. On the other hand, we can view the flip probability as a sort of noise that causes erroneous decoding of the transmitted symbol.

Furthermore, it is memoryless. Transmitted symbols are independent in time. Any transmitted symbol, at time \(t\), does not depend on the previously transmitted symbols (\(t - 1\)).

The capacity of the binary symmetric channel

The capacity of the binary symmetric channel is usually written as

\[ C = 1 - H_b(p), \]

where \(H_b(p) = -p\log_2p - (1-p)\log_2(1-p)\) is the binary entropy function.

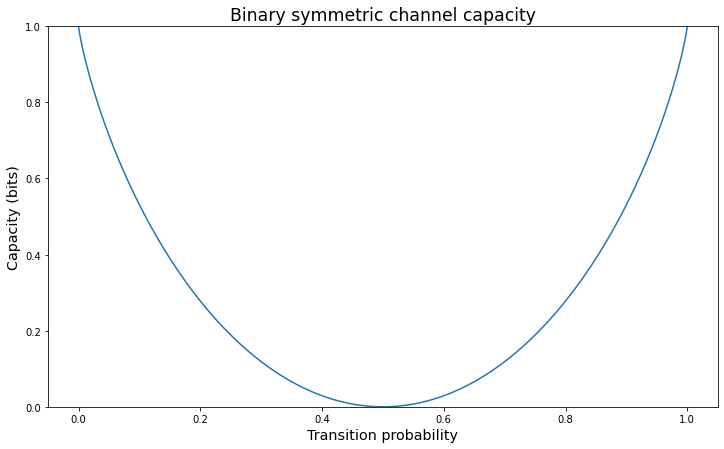
From the capacity illustration, we can observe that, when \(p = 0.5\), the capacity diminishes to 0. This is because we have an equal probability of successful and unsuccessful transmission. In other words, we have no idea whether the transmitted bit was flipped. On the other hand, as \(p \rightarrow 1\) or \(p \rightarrow 0\), we have 100% certainty that the transmission was successful or 100% certainty that the transmitted bit was flipped. That is, we know with absolute certainty what the transmitted symbol (bit) was. This makes the channel capacity \(C = 1\) bit per channel use.

Capacity derivation

We begin by investigating the BSC capacity by defining the channel capacity using the mutual information maximizing input distribution.

\[ C = \max_{p_X(x)} I(X;Y) \]

Let's write out \(I(X; Y)\) in such a way that we can see how it depends on the input distribution \(p_X(x)\). We start by using the definition of mutual information \(I(X; Y)\) via conditional entropy

\[ I(X;Y) = H(Y) - H(Y|X) \]

We can dig deeper into the conditional entropy and see how it relates to the BSC transition probabilities

\[
\begin{array}{rl}
H(Y|X) =& \displaystyle \sum_{x \in \{0, 1\}} p_{X(x)} H(Y|X = x) \\
=& \displaystyle \sum_{x \in \{0, 1\}} p_{X(x)}
\left(
- \sum_{y \in \{0, 1\}} p(y|x) \log(p(y|x))
\right) \\
=& \displaystyle \sum_{x \in \{0, 1\}} p_{X(x)}
\left(
- p \log(p) - (1-p)\log(1 - p)
\right) \\
=& \displaystyle \sum_{x \in \{0, 1\}} p_{X(x)} H_b(p) \\
=& \displaystyle H_b(p) \sum_{x \in \{0, 1\}} p_{X(x)} = H_b(p)
\end{array}
\]

Here, \(H_b(p) = -p\log(p) - (1-p)\log(1-p)\) denotes the binary entropy function. Note that it does not depend on the input distribution. The only thing in the mutual information that depends on the input distribution is \(H(Y)\).

Uniform distribution maximizes entropy. Thus, \(H(Y)\) hits the maximum (\(H(Y)\) = 1), when the output distribution \(p_Y(y)\) is uniform. Now, we can a relationship between the input and output distributions of symmetric channel models, which states that uniform input results in uniform output distribution. Thus, by choosing \(p_X(x)\) to be uniform, we maximize \(H(Y)\) and the mutual information.

This yields the capacity of the binary symmetric channel as

\[ C = \max_{p_X(x)} I(X;Y) = \max_{p_X(x)} \left( H(Y) - H_b(p) \right) = 1 - H_b(p)\]

This very compact capacity formulation perfectly binds the capacity to the transition probability. It is also intuitive that the transition is inherently a Bernoulli process, which is implied by the binary entropy function.

Applications

While the model is simple, it has many real-life applications. Obviously, there are applications in communications theory. In addition, there are other areas, where the binary transition process of BSC is helpful.

One simple application is to model a hard drive write process. There is a non-zero probability for bit flipping. We can study, for instance, the performance of error detection / correcting codes for hard drives using the binary symmetric channel model.

The channel model

The capacity of the binary symmetric channel

Capacity derivation

Applications

Further reading